Astronomische Koordinaten
So wie auf der Erdkugel können auch auf der Himmelskugel Koordinatensysteme festgelegt werden. Die astronomischen Koordinaten ermöglichen die genaue Angabe eines Punktes auf der Himmelskugel. Es gibt verschiedene Koordinatensysteme, doch handelt es sich in der Regel um Kugelkoordinaten. Bei diesen Koordinaten handelt es sich fast ausschließlich um Winkelangaben, wobei die Scheitelpunkte dieser Winkel zumeist im Kugelmittelpunkt, also beim Beobachter, angelegt sind.
Bei allen astronomischen Kugelkoordinaten bilden die Achse und die Grundebene sowie ein frei wählbarer Leitpunkt auf dem Grundkreis, welcher sich als Schnittlinie der Grundebene mit der Kugel ergibt, die Basis. Die Achse und die Grundebene stehen senkrecht aufeinander und verlaufen durch den Kugelmittelpunkt. Die Verlängerung dieser Achse durchstößt die Kugel an zwei Punkten. Diese Durchstoßpunkte werden als die Pole des Kugelkoordinatensystems bezeichnet. Die Grundebene teilt die Kugel in zwei Hälften. Im Falle der astronomischen Kugelkoordinatensysteme kann die Grundebene zum Beispiel der Horizont oder der Himmeläquator sein. Im ersten Fall durchstößt die Achse den Zenit und den Nadir an der Himmelskugel, im zweiten Fall durchstößt die Himmelachse als Verlängerung der Erdachse den nördlichen und den südlichen Himmelspol. Der Abstandswinkel von der Grundebene und der Richtungswinkel, welcher von einem bestimmten Leitpunkt aus gemessen wird, bilden die Koordinaten.
Das Horizontsystem
Beim Horizontsystem wird die Grundebene durch die Horizontebene bzw. der Grundkreis durch den Horizont des Beobachters gebildet. In diesem System bilden der Zenit und der Nadir die beiden Pole. Als Leitpunkt dient in der klassischen Astronomie der Südpunkt, durch den der Himmelsmeridian verläuft. In anderen Bereichen der Astronomie, etwa der Radioastronomie, wird auch der Nordpunkt verwendet. Die Koordinaten heißen Höhe und Azimut. Bei der Höhe handelt es sich um den Abstandswinkel bzw. den Winkelabstand des Gestirns vom mathematischen Horizont. Genau am Horizont beträgt der Winkel 0°, am Zenit, der maximal möglichen Höhe, beträgt der Winkelabstand 90°. Im Falle des Azimut handelt es handelt es sich um den Richtungswinkel bzw. den Winkelabstand des Schnittpunktes zwischen dem Vertikalkreis und dem Horizont vom Leitpunkt. Gezählt wird vom Südpunkt aus in Richtung Westen bzw. vom Nordpunkt aus in Richtung Osten (0° bis 360°). Im ersten Fall sind der Südpunkt 0°, der Westpunkt 90°, der Nordpunkt 180° und der Ostpunkt 270°. Im letzten Fall sind der Nordpunkt 0°, der Ostpunkt 90°, der Südpunkt 180° und der Westpunkt 270°. Die Höhe eines Gestirns kann auch durch den Abstand vom Zenit angegeben werden. In diesem Fall wird von der Zenitdistanz z gesprochen. Wenn h die Höhe des Gestirns bezogen auf den Horizont ist, dann gilt für die Zenitdistanz z:
z = 90° – h
(1)
Gestirne mit einer negativen Höhe bzw. mit h ˂ 0° befinden sich unter dem Horizont. Das Horizontsystem ändert sich in Abhängigkeit vom Ort und Zeitpunkt der Beobachtung. Die Polachse hängt zum einem vom Beobachtungsort ab. Zum anderen Ändern sich die Höhe und das Azimut eines Gestirns aufgrund der Erdrotation mit der Zeit. Zwar kann die Lotrichtung, die Richtung der Polachse, sehr genau bestimmt und damit eine hohe Koordinatengenauigkeit erreicht werden. Allerdings können keine orts- und zeitunabhängigen Koordinaten für Gestirne angegeben werden.
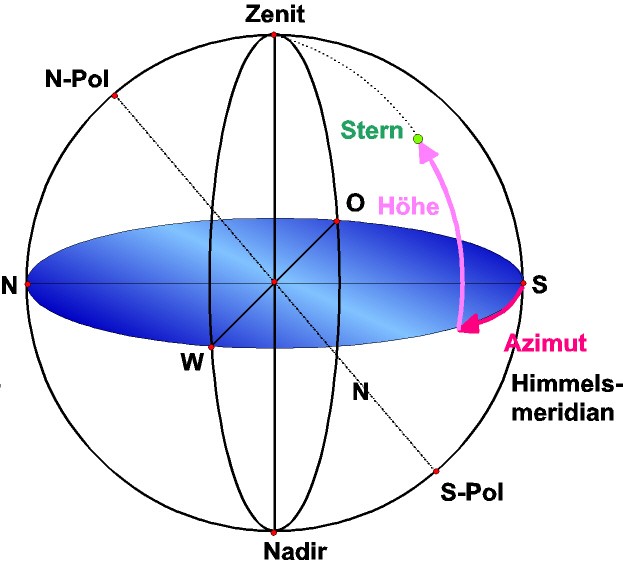
Bild: Das Horizontsystem / Quelle: Wikipedia
Das Äquatorsystem
Mit dem Äquatorsystem werden die Nachteile des Horizontsystems nach und nach behoben. Grundkreis ist der Himmelsäquator und die Polachse verläuft durch den nördlichen und den südlichen Himmelspol. Allerdings gibt es zwei Systeme, das ruhende und das rotierende Äquatorialsystem.
Im ruhenden Äquatorialsystem gilt der südliche Schnittpunkt des Himmelsäquators mit dem Himmelsmeridian als Leitpunkt. Insofern besteht hier noch eine gewisse Vergleichbarkeit mit dem Horizontsystem, nur dass die jeweiligen Grundkreise (Horizont und Himmelsäquator) verschieden sind. Der Leitpunkt des ruhenden Äquatorsystems ist Orts- und Zeitabhängig, er befindet sich für einen bestimmten Beobachter in Ruhe und nimmt nicht an der Drehung der Himmelskugel teil. Der Abstandswinkel vom Himmelsäquator wird als Deklination δ bezeichnet und in Gradmaß angeben. Nach Norden wird die Deklination positiv, nach Süden negativ gezählt. Der Himmelsäquator selbst hat definitionsgemäß die Deklination 0°. Der Richtungswinkel, der Abstand vom Leitpunkt, im ruhenden Äquatorsystem wird wie im Falle des Horizontsystems von Süd nach West gezählt und als Stundenwinkel bezeichnet. D.h. der Stundenwinkel wird in Richtung der scheinbaren Drehung des Sternenhimmels gezählt. Genau im Himmelsmeridian als Leitpunkt hat ein Gestirn den Stundenwinkel 0°. Im Westpunkt hat es den Stundenwinkel 90°, im Nordpunkt einen von 180°, usw. Ebenso wie im Horizontsystem können auch im ruhenden Äquatorsystem keine absoluten Koordinaten für ein Gestirn angegeben werden. Diesen Nachteil behebt erst das rotierende Äquatorialsystem. Ein Nachteil des Äquatorsystems ist, dass die direkte Messung seiner Koordinaten nur mit eingeschränkter Genauigkeit möglich ist.

Bild: Das ruhende Äquatorsystem / Quelle: Wikipedia

Bild: Das ruhende Äquatorsystem für einen Beobachter / Quelle: Wikipedia
Im rotierenden Äquatorialsystem ist der sogenannte Frühlingspunkt als Leitpunkt des Systems festgelegt. Hierbei handelt es sich um einen der beiden Schnittpunkte zwischen der scheinbaren Sonnenbahn am Sternhimmel, der sogenannten Ekliptik, mit dem Himmelsäquator. Im Frühlingspunkt überschreitet die Sonne den Himmelsäquator von Süd nach Nord. Damit endet auf der Nordhalbkugel der Erde auch der kalendarische Winter und der kalendarische Frühling beginnt. Der Frühlingspunkt liegt im Sternbild der Fische und nimmt an der Drehung der scheinbaren Himmelskugel teil. Nun haben wir ein vollständiges Koordinatensystem, welches an der Drehung des Sternhimmels teilnimmt. Wie im ruhenden Äquatorsystem wird der Abstandswinkel als Deklination δ bezeichnet und in Gradmaß angegeben. Hier verhält sich alles genauso wie im Falle des ruhenden Äquatorsystems. Der Richtungswinkel, der Abstand eines Gestirns vom Frühlingspunkt, wird als Rektaszension bezeichnet und entgegen der täglichen Drehung der scheinbaren Himmelskugel gezählt. Allerdings wird hierfür in der Regel nicht mehr ein Gradmaß verwendet, sondern ein Zeitmaß von 0 bis 24 Stunden, wobei sich eine Stunde in 60 Minuten und eine Minute in 60 Sekunden unterteilt. Allerdings wird in seltenen Fällen die Rektaszension auch in Gradmaß (0° bis 360°) angegeben. Das rotierende Äquatorsystem ist unabhängig vom Ort und vom Zeitpunkt der Beobachtung. Die Gestirne haben festgelegte Koordinaten in diesem System. Mit Hilfe der aktuellen Sternzeit, welche nachfolgend erläutert wird, können die Gestirne zu einem bestimmten Zeitpunkt an einem bestimmten Ort an der scheinbaren Himmelskugel aufgefunden werden. Hierbei ist die Summe aus dem Stundenwinkel τ des Gestirns und seiner Rektaszension α gleich der Sternzeit Θ:
Θ = α + τ
(2)

Bild: Das rotierende Äquatorsystem / Quelle: Wikipedia
Der Stundenwinkel τ eines Gestirns hängt natürlich von der geografischen Länge und dem Beobachtungszeitpunkt ab. Die Sternzeit ist gleich dem Stundenwinkel des Frühlingspunktes. Wenn der Frühlingspunkt durch den Himmelsmeridian geht, dann beträgt die Sternzeit = 0:00 Uhr.

Bild: Das rotierende Äquatorsystem für einen Beobachter / Quelle: Wikipedia
Das Ekliptiksystem
Im Ekliptiksystem ist der Grundkreis die Ekliptik, welche die scheinbare Bahn der Sonne an der scheinbaren Himmelskugel ist. Damit ist die Ekliptik auch die Erdbahnebene, auf welche sich auch die Neigungen der Planetenbahnen um die Sonne beziehen. Da diese relativ gering sind, bewegen sich auch alle Planeten des Sonnensystems im Bereich der Ekliptik an der scheinbaren Himmelskugel. Der Mond bewegt sich ebenfalls in diesem Bereich. Die Achse des Systems verläuft durch den Beobachter und steht senkrecht zur Ekliptikebene bzw. Erdbahnebene. Die beiden Durchstoßpunkte der Achse der Ekliptik an der scheinbaren Himmelskugel werden als Pole der Ekliptik bezeichnet. Es gibt einen nördlichen Pol der Ekliptik, welcher sich im Sternbild des Drachen befindet und einen südlichen, welcher sich im Sternbild Goldfisch befindet. Alle Großkreise, welche die Pole der Ekliptik durchlaufen, schneiden die Ekliptik im rechten Winkel. Diese werden als Längenkreise bezeichnet. Auch im Falle des Ekliptiksystems wird der Frühlingspunkt als Leitpunkt verwendet. Die Koordinaten des Systems werden als ekliptikale Breite β und als ekliptikale Länge λ bezeichnet. Die ekliptikale Breite ist der Abstandswinkel bzw. der Winkelabstand eines Gestirns von der Ekliptik. Wie im Falle der Deklination wird dieser in Gradmaß angegeben, nach Norden positiv und nach Süden negativ gezählt. Die ekliptikale Länge ist der Richtungswinkel bzw. der Winkelabstand des Schnittpunktes zwischen dem Längenkreis eines Gestirns und der Ekliptik vom Frühlingspunkt. Wie im Falle der Rektaszension wird dieser entgegen der scheinbaren Drehung der Himmelskugel bzw. der Gestirne am Himmel gezählt, jedoch in Gradmaß angegeben. Das Ekliptiksystem wird vor allem für die Beschreibung der Bewegungen von Objekten des Sonnensystems verwendet.
Das Heliozentrische System
Im Gegensatz zum Ekliptiksystem befindet sich der Mittelpunkt des Heliozentrischen Systems, durch welchen die Achse verläuft, nicht im Beobachter sondern im Sonnenmittelpunkt. Den Grundkreis des Systems bildet wiederum die Ekliptik, die Pole sind wiederum die beiden Pole der Ekliptik. Der Leitpunkt des Systems ist auch wieder der Frühlingspunkt. Die Koordinaten des Systems sind wie im Ekliptiksystem definiert. Ebenfalls analog erfolgt die Zählung dieser Koordinaten. Die Bezeichnung dieser Koordinaten lautet für den Abstandswinkel „heliozentrische Breite“ und für den Richtungswinkel „heliozentrische Länge“. Ebenso wie das Ekliptiksystem wird das Heliozentrische System für die Beschreibung der Bewegungen von Objekten des Sonnensystems verwendet.
Das Galaktische System
Im Galaktischen System ist die Symmetrieebene der Galaxis (Milchstraße) die Grundebene und der Mittelpunkt dieses Systems liegt im Erdmittelpunkt. Die Schnittebene der Grundebene bzw. der Symmetrieebene der Galaxis mit der scheinbaren Himmelskugel wird als galaktischer Äquator bezeichnet, welcher als Grundkreis des Systems dient. Der nördliche Pol des Galaktischen Systems befindet sich im Sternbild Haar der Berenike, der südliche im Sternbild Bildhauer. Als Leitpunkt dient der Schnittpunkt des galaktischen Äquators mit der Verbindungslinie Sonne – Zentrum der Galaxis. Das Zentrum der Galaxis liegt von der Erde aus gesehen im Sternbild des Schützen. Die Koordinaten des Systems werden als galaktische Breite und als galaktische Länge bezeichnet. Das Galaktische System dient zur Beschreibung der Bewegung und Verteilung von Objekten in der Galaxis, also hauptsächlich von Sternen. Konkret werden die Dynamik und die Verteilung der Sterne im Raum beschrieben. Doch auch die Struktur der Galaxis selbst wird mit Hilfe der galaktischen Koordinaten beschrieben.
Koordinatentransformationen
Die Koordinaten des einen Systems können in die eines anderen Systems umgerechnet werden. In diesem Fall wird von sogenannten Koordinatentransformationen gesprochen. Dies ist oft erforderlich. So ist ein bestimmtes Koordinatensystem zur Beobachtung eines bestimmten astronomischen Objektes geeigneter als ein anderes. Wenn dann jedoch die Koordinaten nur für ein bestimmtes System angegeben sind, dann muss es entsprechend umgerechnet werden. Allen astronomischen Koordinatensystemen ist gemeinsam, dass es sich um Kugelkoordinaten handelt. Die Koordinatentransformation, die Umrechnung der Koordinaten des einen Systems in ein anderes, erfolgt mit Hilfe der Grundgleichungen der sphärischen Geometrie. Nachfolgend zunächst eine Zusammenfassung der bereits eingeführten Größen:
- Deklination δ (Einheit: Grad, nördliche Deklinationen werden positiv und südliche negativ gezählt)
- Rektaszension α (Einheit: Grad)
- Stundenwinkel τ (Einheit: Grad)
- Schiefe der Ekliptik ε (Einheit Grad)
- Ekliptikale Breite β (Einheit: Grad)
- Ekliptikale Länge λ (Einheit: Grad)
- Höhe h (Einheit: Grad)
- Azimut a (Einheit: Grad, gezählt von Süd über West)
- Geografische Breite des Beobachtungsortes φ (Einheit Grad, nördliche Breiten werden positiv und südliche Breiten negativ gezählt)
Für die Umrechnung vom rotierenden Äquatorsystem in das Ekliptiksystem gilt:
tan(α) = [sin(α) ∙ cos(ε) + tan(δ) ∙ sin(ε)] / cos(α)
(3)
sin(β) = sin(δ) ∙ cos(ε) – cos(δ) ∙ sin(ε) ∙ sin(α)
(4)
Für die Umrechnung vom Ekliptiksystem in das rotierende Äquatorsystem gilt:
tan(α) = [sin(λ ∙ cos(ε) – tan(β) ∙ sin(ε)] / cos(λ)
(5)
sin(δ) = sin(β) ∙ cos(ε) + cos(β) ∙ sin(ε) ∙ sin(λ)
(6)
Für die Umrechnung vom ruhenden Äquatorsystem in das Horizontsystem gilt:
tan(α) = sin(τ) / [cos(τ) ∙ sin(φ) – tan(δ) ∙ cos(φ)]
(7)
sin(h) = sin(φ) ∙ sin(δ) + cos(δ) ∙ cos(τ) ∙ cos(φ)
(8)
Für die Umrechnung vom Horizontsystem in das ruhende Äquatorsystem gilt:
tan(τ) = sin(α) / [tan(h) ∙ cos(φ) + sin(φ) ∙ cos(α)]
(9)
sin(δ) = sin(φ) ∙ sin(h) – cos(φ) ∙ cos(h) ∙ cos(α)
(10)
Die Umrechnung des ruhenden und des rotierenden Äquatorsystems untereinander erfolgt mit Gleichung (2). Für die Gleichungen (3), (5), (7) und (9) gilt folgende Quadrantenregel:
Nenner Zähler Ergebnis liegt im
positiv positiv 1. Quadranten
positiv negativ 2. Quadranten
negativ negativ 3. Quadranten
negativ positiv 4. Quadranten
Die Veränderung von Koordinaten
Die Koordinaten eines Gestirns verändern sich aufgrund verschiedener Einflüsse. Diese Einflüsse werden aufgrund der Bewegung der Gestirne, z.B. der Erde um die Sonne, infolge der Verlagerung der Grundebene oder des Leitpunktes des zugrundeliegenden Koordinatensystems und der Erdatmosphäre hervorgerufen. Nachfolgend soll auf verschiedene Einflüsse eingegangen werden.
Das Licht der Gestirne wird beim Durchgang durch die Atmosphäre gebrochen, was als Refraktion bezeichnet wird. Zunächst bewegt sich der Lichtstrahl durch den luftleeren Weltraum. Beim Auftreffen auf die Atmosphäre bewegt sich dieser zunehmend durch die immer dichter werdenden Luftschichten, so dass es zur Refraktion kommt und der Lichtstrahl des Gestirns gekrümmt ist. Das Gestirn erscheint dann nicht mehr exakt in seinen tatsächlichen Koordinaten, wie sie ohne Erdatmosphäre gemessen würden, sondern in Richtung der im Beobachtungsort an die Kurve gelegten Tangenten. Im Ergebnis ist die scheinbare Höhe (gemessen mit Erdatmosphäre) des Gestirns daher größer als seine wahre Höhe (gemessen ohne Erdatmosphäre). Nur im Zenit der Himmelskugel wirkt sich die Refraktion nicht aus. Abhängig ist die Refraktion vom Luftdruck und der Lufttemperatur. Bereits in kleinen Atmosphärenschichten führen schnelle Änderungen der Luftdichte, etwa durch turbulente Strömungen, zu rasch wechselnden Werten für die Refraktion. Neben einer konstanten Refraktion, wie sie durch eine ruhige Atmosphäre hervorgerufen wird, gibt es daher auch eine variable Refraktion. Diese hat eine Amplitude zwischen 0,5 und 5 Bogensekunden (1 Grad (°) = 60 Bogenminuten (`), 1 Bogenminute = 60 Bogensekunden („)) und wird als Richtungsszintillation oder Seeing bezeichnet. Die Frequenz der variablen Refraktion ist kleiner als ein Hertz.
Im Verhältnis zur Lichtgeschwindigkeit von c = 299.792.448 m/s ist die Bahngeschwindigkeit der Erde von rund 30.000 m/s nicht mehr vernachlässigbar. Ähnlich wie senkrecht nach unten fallender Regen von einem schnell fahrenden Auto aus betrachtet mit einem bestimmten Winkel schrägt gegen die Windschutzscheibe auftrifft, ändert sich auch der Einfallwinkel des Lichtstrahls eines Gestirns aufgrund der Bahnbewegung der Erde. Dieser Vorgang wird als Aberration bezeichnet. Im Falle der durch die Bahnbewegung der Erde hervorgerufenen Aberration wird von einer jährlichen Aberration gesprochen, da die Erde für einen Bahnumlauf ein Jahr benötigt. Aufgrund der Bewegung der Erde unterscheidet sich die Beobachtungsrichtung zu einem Gestirn um einen kleinen Winkel, gegenüber der Richtung, in welcher das Gestirn von einer ruhigen Erde aus gesehen würde. Dieser kleine Winkel wird als Aberrationswinkel bezeichnet. Für den Aberrationswinkel σ gilt:
σ = κ ∙ sin(ξ)
(11)
Hierbei ist κ die Aberrationskonstante in Bogensekunden mit dem Wert κ = 20,49552„ und der Winkel zwischen Blickrichtung zum Gestirn und Bewegungsrichtung in Grad. In Folge der Aberration ändern sich die Koordinaten Deklination und Rektaszension eines Gestirns entsprechend mit einer jährlichen Periode. Auf der scheinbaren Himmelskugel beschreibt das Gestirn dann im Laufe eines Jahres eine kleine scheinbare Ellipse. Diese Aberrationsellipse hat die große Halbachse aa und die kleine Halbachse ba. Beide Größen werden in Bogensekunden angegeben. Zusammen mit der ekliptikalen Breite β und der Aberrationskonstanten κ gilt:
aa = κ
ba = κ ∙ sin(β)
(12)
Neben der Bahnbewegung der Erde führt auch die Rotation der Erde zu einer Aberration. In diesem Fall wird von einer täglichen Aberration gesprochen. Die Konstante der täglichen Aberration ist von der geografischen Breite des Beobachtungsortes abhängig. Aufgrund der täglichen Aberration erfolgt die Kulmination eines Gestirns, also sein Durchgang durch den Himmelsmeridian, um einen geringen Betrag verfrüht.
Die Bewegung der Erde um die Sonne wie auch die Erdrotation haben noch einen weiteren Effekt zur Folge, welcher als Parallaxe bezeichnet wird. Aufgrund dieses Effektes beschreiben Sterne kleine Ellipsen an der scheinbaren Himmelskugel. Konkret werden die scheinbaren Bewegungen von Sternen gegenüber weiter entfernten Sternen betrachtet. Bekannt ist, dass sich nahe Objekte gegenüber weiter entfernten Objekten verschieben, wenn der Beobachter seinen Standort wechselt. Beim Fahren mit dem Auto kann das gut beobachtet werden. Die Bäume am Straßenrand huschen schnell vorbei, während die weit entfernten Bäume zunächst kaum ihren Standort zu ändern scheinen. Im Prinzip passiert das auch mit nahen Sternen gegenüber weiter entfernten bei der Rotation der Erde (tägliche Parallaxe) und der Bewegung der Erde um die Sonne (jährliche Parallaxe). Wird ein relativ naher Stern betrachtet, so verändert dieser im Verlauf eines Jahres seine scheinbare Position gegenüber den weiter entfernten Sternen. Der Winkel, unter dem diese Veränderung der scheinbaren Position erscheint, wird mit π bezeichnet. Wenn a die große Halbachse der Erdbahn und r die Entfernung des Sterns von der Sonne ist, so gilt für die jährliche Parallaxe π:
sin(π) = a/r
(13)
Eine Parallaxe von 1„ hätte ein Stern in einer Entfernung von 3,26 Lichtjahren. Der nächste Stern Proxima Centauri ist 4,3 Lichtjahre von der Sonne entfernt. Damit haben alle Sterne eine Parallaxe kleiner als 1„. Die Entfernung von 3,26 Lichtjahren wird als 1 Parsec (pc) bezeichnet. Wenn r in Parsec und π in Bogensekunden angegeben wird, so vereinfacht sich Gleichung (13) zu:
r = 1/π
(14)
Der nächste Stern Proxima Centauri hat mit π = 0,77„ die größte Parallaxe. Mit zunehmender Entfernung des Sterns von der Sonne wird auch seine Parallaxe immer kleiner. Zwischen einem fiktiven Beobachter im Erdmittelpunkt und einem tatsächlichen auf der Erdoberfläche erscheint ein Stern in Blickrichtung auch leicht verschoben. Im Falle einer Erdrotation, also an einem Tag, beschreibt der Stern vor diesem Hintergrund ebenfalls eine kleine Parallaxe. In diesem Fall wird von der täglichen Parallaxe πt gesprochen. Diese ergibt sich aus dem Erdradius R im km, der Entfernung des Sterns zum Erdmittelpunkt in km und der Höhe h des Gestirns in Grad:
πt = [R ∙ cos(h)]/r
(15)
Die tägliche Parallaxe erreicht ihren größten Wert, wenn das Gestirn am Horizont und vom Erdäquator aus beobachtet wird. Der Erdradius ist am Äquator größer als an jedem anderen Ort, so dass auch die tägliche Parallaxe dort am größten ist. Eine entsprechend am Äquator und Horizont gemessene Parallaxe wird als Äquatorhorizontparallaxe bezeichnet.
Präzession und Nutation
Eine weitere Veränderung der astronomischen Koordinaten wird durch die Präzession und die Nutation bewirkt. Die Erde ist keine exakte Kugel, sondern ein Ellipsoid. Die Gravitation von Sonne und Mond greifen an diesen Erdellipsoid an. Dadurch kommt es zu einer langsamen Verlagerung der Erdachse. Dies führt im Ergebnis auch zu einer Verlagerung der Äquatorebene der Erde und damit verändert sich auch die Grundebene des Äquatorsystems. Doch auch die anderen Planeten im Sonnensystem beeinflussen die Erde, so dass sich auch die Lage der Ekliptik ändert. Die Gesamtheit dieser Veränderungen besteht aus einem langperiodischen Anteil, welcher als Präzession bezeichnet wird, und einem kurzperiodischen Anteil, der sogenannten Nutation.
Die Präzession der Erdachse kann mit einem rotierenden Kreisel verglichen werden. Die Schwerkraft greift den Kreisel an, so dass dieser zu Boden kippen würde. Allerdings verhindert die Rotation des Kreisels das Kippen. Im Widerstreit der Kräfte taumelt die Achse und beschreibt dabei einen Umlauf um einen definierten Mittelpunkt. Im Falle der Erdachse ist dies ähnlich. Sonne und Mond greifen gravitativ den Erdellipsoiden an. Die Erdachse fängt an zu Taumeln und beschreibt daher eine Kreisbewegung um einen definierten Mittelpunkt, den Pol der Ekliptik. Eine Periode dauert allerdings 25.800 Jahre. Zum heutigen Zeitpunkt ist die Erdachse auf den Polarstern ausgerichtet. Aufgrund der Verlagerung der Erdachse wird sich das jedoch ändern. Im Jahre 9000 wird der Stern Deneb im Sternbild Schwan die Rolle des Polarsterns einnehmen und im Jahre 13000 der Stern Wega im Sternbild Leier. Aufgrund der Präzession der Erdachse bewegt sich der Frühlingspunkt um 50,37 Bogensekunden pro Jahr auf der Ekliptik zurück. So lag der Frühlingspunkt vor rund 2.000 Jahren noch im Sternbild Widder, weshalb dieser Punkt noch heute als Widerpunkt bezeichnet wird. Heute liegt er im Sternbild der Fische. In der Zukunft wird der Frühlingspunkt in das Sternbild Wassermann wandern. Für einen Gesamtlauf durch die Ekliptik bzw. den Tierkreis benötigt der Frühlingspunkt 25.800 Jahre, eben die Präzessionsperiode der Erdachse.
Aufgrund der Präzession sind das Äquatorsystem und das Ekliptiksystem in der Zeit veränderlich und damit zeitabhängig. Daher müssen die Koordinaten für einen bestimmten Zeitpunkt festgelegt werden. In Sternkarten und Sternkatalogen wird dafür eine bestimmte Normalepoche festgelegt. In der Regel sind das derzeit Anfang 1950 oder Anfang 2000.
Die Präzession wird von einer Schwankung des Himmelspols mit einer Periode von 18,6 Jahren um einen gedachten mittleren Himmelspol überlagert. Dies wird als Nutation bezeichnet. Auch diese wird durch die gravitativen Einflüsse von Sonne und Mond hervorgerufen. Im Ergebnis wird dadurch die durch Präzession hervorgerufene Kreisbahn des Himmelspols um den Pol der Ekliptik zu einer Wellenlänge mit einer Amplitude von wenigen Bogensekunden verzerrt.
Die Sterne haben ebenfalls eine Eigenbewegung. Sie bewegen sich um das Zentrum der Galaxis (Milchstraße). Kurzfristig sind keine Veränderungen feststellbar. Langfristig werden die Sterne am Sternenhimmel aufgrund ihrer Eigenbewegung ihre Positionen verändern und sich damit auch die bestehenden Sternbilder auflösen. Die Eigenbewegung wird in Bogensekunden pro Jahr angegeben. Die größte Eigenbewegung hat Barnards Pfeilstern mit einem Wert von 10,34 „/a.
Die Gestirnsörter
Die Position eines Gestirns an der scheinbaren Himmelskugel wird in Koordinaten angegeben und als sein Ort bezeichnet. Die gemessenen Koordinaten geben den tropozentrischen Ort, also den Ort bezogen auf der scheinbaren Himmelskugel an. Unter Berücksichtigung der Refraktion sowie der täglichen Aberration und der täglichen Parallaxe ergibt sich zunächst der scheinbare Ort. Hierbei ist noch zu erwähnen, dass die tägliche Parallaxe nur bei astronomischen Objekten des Sonnensystems messbar ist. Der wahre Ort eines Gestirns ergibt sich erst unter Berücksichtigung der jährlichen Aberration und der jährliche Parallaxe. Der mittlere Ort eines Gestirns ergibt sich, wenn die Nutation berücksichtigt wird. Durch Berücksichtigung der Präzession kann der mittlere Ort korrigiert werden, so dass sich der wahre Ort für einen bestimmten Zeitpunkt (eine bestimmte Normalepoche) ergibt.
Sternkarten und Sternkataloge
Auf Basis von Sternkatalogen werden Sternkarten für verschiedenste Zwecke erstellt. Eine Sternkarte ist die Darstellung eines Teils oder der gesamten scheinbaren Himmelskugel mit allen beobachtbaren Objekten bis zu einer bestimmten Gesamthelligkeit. Eine Sternkarte kann für einen bestimmten Zeitpunkt angegeben werden und dann auch alle zeitlich veränderlichen Objekte, etwa die Position der Planeten des Sonnensystems, beinhalten. Wenn eine Sternkarte allerdings für einen längeren Zeitraum gelten soll, dann dürfen die zeitlich veränderlichen Objekte nicht eingetragen werden. Streng genommen ändern sich aufgrund der Eigenbewegung auch die Positionen der Sterne, so dass eine Sternkarte, wie bereits erwähnt wurde, immer für eine bestimmte Normalepoche gilt. Derzeit sind dies die Normalepochen 1950 und 2000. Allerdings sind die Änderungen bezogen auf ein Menschenleben relativ klein, so dass sie nicht weiter auffallen.
Grundlage für jede Sternkarte ist ein astronomisches Koordinatensystem. In der Regel wird das rotierende Koordinatensystem verwendet, gelegentlich auch das Ekliptiksystem oder das galaktische System. Sternkarten können auf verschiedene Weise erstellt werden. Von Hand gezeichnet, maschinell bzw. computertechnisch erstellt oder auf fotografischem Wege erstellt werden. Eine besondere Form ist die drehbare Sternkarte, die besonders im Amateurbereich zur schnellen Orientierung am Sternhimmel verwendet wird. Auf einer drehbaren Sternkarte ist der ganze Sternenhimmel im Verlauf eines Jahres dargestellt. Mit Hilfe einer Maske wird allerdings nur der Teil des Sternenhimmels gezeigt, welcher zu einem bestimmten Zeitpunkt zu sehen ist. Der andere, zu diesem Zeitpunkt nicht sichtbare Teil des Sternhimmels, ist dann verdeckt. Am Rand der Sternkarte befinden sich Skalen, insbesondere Monat, Tag und Uhrzeit. Mit Hilfe dieser kann der sichtbare Himmelsausschnitt auf der drehbaren Sternkarte für einen bestimmten Monat, Tag und Zeitpunkt eingestellt werden. Genähert lassen sich mit Hilfe dieser Skalen auch die Aufgangs-, Kulminations- und Untergangszeiten von Gestirnen bestimmen. Drehbare Sternkarten können auch astronomische Koordinatennetze, etwa des ruhenden Äquator- oder des Horizontsystems, beinhalten. Bei Angabe beider Koordinatensysteme ist auch eine näherungsweise Transformation von astronomischen Koordinaten von einem System in das andere möglich.
Kurz erwähnt wurde bereits, dass Sternkarten auf Basis von Sternkatalogen erstellt werden. Sternkataloge enthalten für ausgewählte Gruppen von Sternen bestimmte Einzeldaten, wie etwa deren Koordinaten oder Helligkeiten. Doch viele andere physikalische Einzeldaten können Eingang in Sternkatalogen finden. In der Regel beinhalten Sternkataloge alle Sterne bis zu einer bestimmten Grenzhelligkeit in einem größeren Bereich der scheinbaren Himmelskugel. Sternkataloge, welche einen bestimmten Bereich der scheinbaren Himmelskugel erfassen, werden als Durchmusterungen bezeichnet. Sternkataloge, welche die Position der Sterne mit hoher Genauigkeit angeben, werden als Fundamentalkataloge und Positionskataloge bezeichnet.

Bild 1-6: Der nördliche Sternenhimmel / Quelle: http://www.sternfreunde-muenster.de